Глава 3 Материализация сакральной геометрии

We use cookies. Read the Privacy and Cookie Policy

Глава 3

Материализация сакральной геометрии

В этой главе мы попытаемся соединить знания сакральной геометрии с материальными носителями ее свойств. Геометрические фигуры, «витающие» в пространстве и начертанные на бумаге, в этой главе начнут переходить в трехмерный мир и материализовываться. Мы воочию увидим, как происходит рождение материи из геометрического мира. Нарушенная зеркальная симметрия, послужившая началу нашего мира, в сакральной геометрии отражена практически полностью, но имеет место недоговоренность, недосказанность, также осталась не раскрытой генетическая связь. Как мы теперь знаем, правая и левая половины тела, по сути, добрые соседи, но не одно и то же. Головной мозг, отделившийся и возвысившийся над туловищем, поменял левое на правое. После того, как он стал «пространственным» перебежчиком, правое полушарие стало руководить левой стороной, а левое — правой. Этот перехлест необходим для стабилизации динамичных автоморфичных структур на разных этажах и разных уровнях Живой субстанции. Принцип подобия говорит о том, что подобная инверсия сторон в Живой субстанции начинается с уровня геометрии и потом переходит на уровень атомов и молекул. Причем внутреннее пространство Живой субстанции радикально отличается от внешнего. О существовании этого правила люди догадывались с древних времен. В различных восточных учениях латеральности (сторонам) придавали огромное значение. Таким образом, люди пытались «помирить» внешнее и внутреннее пространство Живой субстанции. Правая сторона отдавалась женскому началу, а левая всегда считалась мужской стороной. В Египте, например, символом школы Эхнатона стал правый глаз Гора, контролируемый левым полушарием. Это мужское знание, логическая сторона творения мира, представление о том, как дух создал все. Вот первый стих из «Книги Бытия»: «. и Дух Божий носился над водою». Однако есть одна вещь, о которой не говорится в Библии, но которой уделяли особое внимание в школе Эхнатона: для того чтобы дух мог двигаться в пустоте, он должен был двигаться по отношению к чему-то. А в буддизме есть изречения: «О, великая пустота!», «Пустота есть форма, форма есть пустота». Эммануил Кант также пытался ответить на вопрос правое-левое, понимая пустоту по-своему. Луи Пастер, к великому сожалению, так и не смог ответить, что же это такое. Диссимметрия, которую он обнаружил, также укладывается в эту категорию, но почти не поддается пониманию, исходя из логических конструкций. Попробуем и мы разрешить вековые загадки мироздания. Вот как интерпретирует сакральную геометрию Друнвало Мельхиседек. В Великой Пустоте не существует ничего. Как можем мы узнать о движении в ней духа, если v нас нет точки отсчета? Вот как решала эту загадку школа Эхнатона: дух проецирует себя в шести направлениях — вверх и вниз, вперед и назад, вправо и влево. Это можно отразить при помощи осей координат, обозначив их как X, Y и Z. Расстояние проекций не имеет значения, хватит и одного дюйма. Таким образом, дух проецируется в шести направлениях. Следующий шаг — соединить линии таким образом, чтобы вначале образовался квадрат, а затем пирамида. После этого следует продлить линии и получить нижнюю пирамиду. Обе пирамиды дадут нам октаэдр. Теперь дух получает реальность, заключенную в октаэдре. И хотя это лишь умозрительный образ, он дает нам представление о движении, так как границы уже установлены. Затем дух начал совершать вращательное движение по отношению к трем осям, описывая сферу. В сакральной геометрии прямая линия считается мужской, а кривая — женской. Таким образом, вращая октаэдр, дух превратился из мужчины в женщину, то есть в сферу. В Библии говорится, что первым был создан мужчина, а после него женщина. Это и есть изменение прямолинейного движения на круговое. Дух изменил характер движения потому, что необходимая для творения геометрическая прогрессия соответствует кривым, или женским, линиям. Итак, Дух Божий находится в сфере, но куда он несся? Во всей Вселенной было только одно известное место — поверхность. Поэтому ученикам школы Эхнатона говорили, что дух двигался к поверхности. Неважно, к какому именно месту поверхности, главное, что к поверхности. Это было первое движение из Великой Пустоты. (Как мы помним, процесс клеткообразования в системе белок-вода происходит только на адгезивной поверхности.) После первого движения каждое последующее движение происходит автоматически. Каждое предыдущее подсказывает последующее, и так продолжается до тех пор, пока не будет создана Вселенная. Когда дух оказался на поверхности, единственное, что ему оставалось, это создать вторую сферу. То, что получилось, известно, как vesica piscis, или взаимопроникающие сферы — метафизическая структура, стоящая за светом. Это был первый день Творения. Пересекаясь, две сферы образуют круг или овал. Входя в этот новый круг и образуя следующую сферу, вы получите образ второго дня Творения. После этого вращательное движение продолжается на поверхности сферы, пока та не будет создана окончательно. Когда вы доходите до шестого дня Творения, то получаете шесть кругов, идеально соединенных друг с другом. На седьмой день дух отдыхает, так как творение завершено, и все законы Вселенной созданы. Когда этот образ приобретает вихревое движение, трехмерные объекты перестают вписываться в схему. Вот почему важно понимать то, что предмет сакральной геометрии — это не просто линии на бумаге, а, скорее, движение духа в Великой Пустоте. Необходимо создать карту движения трехмерной Великой Пустоты для нашей планеты. Существуют сто сорок четыре различные формы пустоты, в зависимости от того, на каком обертоне находитесь вы. Первый образ, который вы получите, — трубчатый тор. Он возникает во время первого вращения или первых шести дней Творения. Вращая паттерн, вы создаете этот образ (трубчатый тор с микроскопическим отверстием в центре). Помните, что речь идет о трехмерном образе, а не о двумерном изображении. Трубчатый тор — первичная форма Вселенной. Его уникальность состоит в том, что он движется в самом себе, никакая иная форма не способна на это. Стэн Тенен, посвятив двадцать лет исследованиям, сумел проследить форму трубчатого тора и, убрав незначительные детали, развернул его в виде спирали. Затем он расположил полученную спираль в трехмерном тетраэдре. Пропуская свет сквозь эту структуру под разными углами, ученый определил, что отбрасываемая тень повторяет все буквы древнееврейского алфавита. Он также обнаружил, что, расположив структуру иначе, может тем же способом воспроизвести все греческие, а также арабские буквы. Существует 27 таких симметричных позиций. Таким образом, первое, что мы узнаем из «Книги Бытия», — это связь между языком и метафизической формой. С этим не согласиться невозможно! Всё взаимосвязано! Существует только одна объективная реальность и множество способов ее интерпретации. На самом же деле количество возможных интерпретаций событий — бесконечно. Чтобы понять, что древние существа этого мира были, наверное, более развиты, чем мы думаем, давайте возьмем фонетический перевод санскритского стихотворения «О, Господь Кришна, умащённый йогуртом поклонения молочниц, О спаситель падших, О, господин Шивы, защити меня!». Исследователи обнаружили, что у каждого из звуков санскрита есть числовое соответствие (в иврите, калмыцком языке буквы также несут числовую нагрузку). Так вот, каждому из звуков на санскрите есть числовое соответствие от ноля до девяти, некоторые же слоги имеют два числовых соответствия. Например, ка, исходный звук, переводится как дух та соответствует числу ноль либо один, наверное, в зависимости от его использования. Когда исследователи взяли эти различные значения звуков и сопоставили их именно с этим стихотворением, то получилось исключительной важности математическое число — 0,3141592653589, продолжающееся до тридцать второго знака. Это число Пи, поделенное на десять с точностью до тридцать второго знака! 32, как мы помним, число кристаллических классов и среднее число звуков-букв в человеческих языках. Тоже, казалось бы, странные совпадения. Но в нумерологии нет странностей, а есть только законы. Теперь вернемся к математической «бесконечности». Никто до сих пор не выяснил, как рассматривать запятую в этой десятичной дроби, поэтому число представлено как Пи деленное на десять. Если сдвинуть запятую десятичной дроби направо на один знак, получим 3,1415…, длина окружности, деленная на диаметр. Допустим, они могли знать об окружности, деленной на диаметр, но по представлениям нашей культуры о том, кем были эти древние, нет никакой возможности поверить в то, что они могли рассчитать это с такой точностью. И всё-таки это неоспоримое доказательство. На санскрите есть много подобных стихотворений. Итак, вначале было Слово. Это можно расценить как вибрацию и звуковые волны в космосе.

Давайте взглянем на саму модель Творения. С математической точки зрения, она состоит из минимального количества линий, необходимых для того, чтобы очертить на плоской поверхности трёхмерную форму, именуемую тором. Тор здесь — трубчатый тор, поскольку сформирован как внутренняя трубка — и уникален своей способностью сворачиваться внутрь или разворачиваться наружу. Во всём сущем мире ни одна другая форма такое или нечто подобное проделывать не может. Артур Янг (Arthur Young) обнаружил, что на этой форме можно выделить семь областей, которые были названы семицветной картой. Возьмите почти любую книгу по математике и в разделе о торе вы найдёте, что это семь областей, все одного размера, которые в трубчатом торе точно совпадают. Происходит это тем же образом, как на модели Бытия, где шесть кругов обходят вокруг седьмого, центрального, тем самым, охватывая всю поверхность. В сакральной геометрии существует понятие, именуемое движением по зубчатому колесу. Вы берёте круг или линию и сдвигаете его/её по трещётке, словно пользуетесь храповиком из механизма какой-либо машины. Представьте себе две модели Бытия, наложенные друг на друга, одна из которых зафиксирована. Если вы повернёте другую модель на 30 градусов, то получите двенадцать сфер вокруг одной центральной. В двух измерениях это будет выглядеть как двумерный тор. В трёх измерениях будет иметь вид трубчатого тора. Если все возможные линии соединить в середине, получится развернутый тор. Сдвинув эти двенадцать сфер по зубчатому колесу ещё раз, теперь на 15 градусов, так, чтобы сфер стало 24, получим трансцендентальную модель (в нумерологии число 24 — это факториал числа 4, или частота смены кадров в кинематографе. Четверка — прорыв в другое измерение, которое считают временем. 24 кадра в секунду говорят о фиксации этого измерения человеческим мозгом).

Что такое трансцендентальная модель? Трансцендентальным числом в математике является число, исходящее из иного измерения. В том измерении оно, вероятно, существует как целое, но, проникнув сюда, целиком в этот мир не переносится. У нас таких чисел — множество. Одно из них, например, греческое (фи — phi ratio) ф — пропорция. Это — математическое соотношение, начинающееся с 1,6180339 и продолжающееся бесконечно — в том смысле, что никогда не известно, какой будет следующая цифра: компьютеры считали месяцами, но до конца так и не дошли. Трансцендентальные числа, судя по всему, являются связующим звеном между числовым полем (целыми числами) и сакральной геометрией. Форма тора управляет многими аспектами нашей жизни. Например, сердце человека состоит из семи мышц, образующих тор, и перекачивает кровь в семь областей, указанных на карте тора. Тор существует вокруг всех жизнеформ, всех атомов и всех космических тел, таких как планеты, звёзды, галактики и т. д. Это — основная форма в Бытии. На рис. 9 вы впервые видите документальное подтверждение начала «развертки» тора в плазме крови. Это двумерное проявление тора в сыворотке крови больного раком. Начальная стадия заболевания. У больного пока нет никаких жалоб и признаков рака, но кровь уже сигнализирует о том, что в организме начались процессы перехода Живого вещества в двумерное состояние. Через полгода у него установлен рак толстой кишки. Стоит обратить внимание на темные маленькие треугольники, напоминающие фракталы «сита Серпинского». Абсолютно четкие треугольники внутри листоподобных структур — дело «рук» сакральной геометрии. На этом наглядном примере видно, как «сожительствуют» фрактальная и сакральная геометрия с Живой субстанцией. Стоит учесть, что мы использовали сыворотку крови, а в ней как известно, нет ДНК и РНК. Поэтому утверждать, что Живое началось с ДНК и РНК — опасное заблуждение, которое уводит биологию от истины. Скорее надо говорить, что Живая субстанция исходит из пространства, из полевых структур, содержащих сакральные фигуры и фрактальные элементы.

Рис. 9. Проявление элементов двухмерного тора и «сита Серпинского» в сыворотке крови, (фото 20x40).

Очень ярко проявляют себя законы геометрии на уровне простейших. Они словно скроены по шаблонам и лекалам линейной геометрии (Рис. 10).

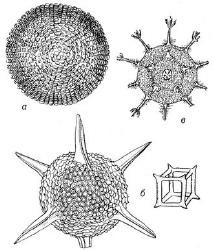
Рис. 10. Сакральная геометрия в диатомовых.

Теперь вновь вернемся к Сотворению мира. Вопрос: наш мир произошел из двухмерного плоского или из одной точки? На него может ответить феномен пересечения трех колец. Каким образом кольца могут пересекаться, и при каких условиях это невозможно? Они не пересекаются, если представляют собой окружности, нарисованные линией, и число их четное. Если они «прорисованы» плоскостью и нечетные, картина иная. Кажется, что если все время рисовать и сдвигать кольца в одной плоскости, они не перехлестываются друг с другом. Однако это не совсем так. Если они широкие, то процесс вытеснения колец из двухмерного пространства можно увидеть воочию на примере трех колец. (Рис. 11) Стало быть, ширина плоскости влияет на пересечение плоскостей, и необязательно они должны быть в виде круга.

Рис. 11. Непересекающиеся кольца.

Как видим, соседние кольца наложены друг на друга и не сцеплены друг с другом, а третье кольцо соединяет их, но в то же время не соединено с соседним. Если изображать круги разноцветными, круглыми или плоскими, то «номер» с появлениями всех (особенно круглых) сакральных фигур не пройдет. Для изображения процесса появления и развития мира изначально годятся только линии и точки. Объемные и плоские формы не годятся ввиду того, что они не в состоянии переходить через пространства, доступные линиям и точкам. Объемные формы проявляются только тогда, когда линии и точки начинают двигаться. Но кто их сдвинет с «мертвой точки»? На бумаге — геометр, а в реальном пространстве — физика. Поэтому можно предположить, что изначально форма констатирует наличие физического тела в пространстве. Обратное не представляется возможным.

Закончив проекцию первых семи сфер, Сознание продолжает движение по вращательной модели до тех пор, пока не завершит своего второго вихревого движения, создав трёхмерную форму, которую можно держать в руках. Самое интересное, что почти никто в «опытах» на бумаге не указывает направление вращения, что в принципе неверно. В случае с Жизнью направление вращения любого объекта (геометрического и физического) имеет первостепенное значение. Геометр же с окружностями может произвольно стирать линии и передвигать кольца в любую сторону. Однако, в этих геометрических «изысках» все же есть рациональное зерно.

Если стереть все линии в середине, можно увидеть модель из сфер подобную той, которую дух увидел бы, если бы вышел наружу из своего творения. Восьмая сфера находится точно за видимыми сферами. Если соединить их центры, можно увидеть куб. Древние называли эту гроздь сфер Яйцом Жизни. Яйцо Жизни является морфогенетической структурой, создавшей тело. Всё наше физическое существование зависит от структуры Яйца Жизни. Всё в вас сотворено через форму Яйца Жизни, до самого цвета ваших глаз, формы вашего носа, длины ваших пальцев и т. д. Всё основывается на этой единственной форме. Подобное изображение можно встретить и в буддийской ритуальной графике, и в китайских произведениях искусств. Можно согласиться с Мельхиседеком насчет единственной формы, но некоторые «формы» не совсем вписываются в автоморфизмы человека. Где, например, основополагающая пентагональная симметрия в Яйце Жизни? Яйцо Жизни, однако, подтверждает нашу теорию о наличии «разрешенных» в физике твердого тела осей симметрии в Живой субстанции. Возможно, мы увидим пентагональную симметрию или ее «следы» в окружающем пространстве при разворачивании этих сакральных фигур. Тогда все станет на свои места. В этом случае видны места соединения не только среды с пространством Живого существа, но и «сосуществование» всех осей симметрии.

Приступим теперь к обсуждению схемы вихревого вращения энергии (на бумаге). Каждый раз при завершении вращательного движения возникает новая форма, и эта форма становится основой творения. Вращение всегда начинается из внутренних мест. Однако направление вращения вновь не указывается. Яйцо Жизни — двумерное изображение трехмерной фигуры. Яйцо Жизни — формула гармонии музыки и электромагнитного спектра. Формула всех без исключения структур. Следующее вращение даст нам контур или необходимое количество кругов для создания Цветка Жизни. Этот цветок состоит из семи кругов. Следующий вихрь есть третий поворот. Если внимательно глядеть на Цветок Жизни, можно увидеть семь кругов, касающихся друг друга. Всего в Цветке Жизни содержится девятнадцать кругов (Рис. 12), которые окружены двумя концентрическими кругами.

Рис. 12. Цветок Жизни

По какой-то причине это изображение находят во всём мире. Почему останавливаются именно на девятнадцати кругах? Это же бесконечная сетка, и её можно было бы прервать в любом месте. В Китае его вписывали в прямоугольную форму, перенося модель всё дальше и заполняя так прямоугольник до самых его краёв. «Инопланетяне» также не прочь «порисовать» этот цветок (со своими «изысками») на полях. Если учесть, что диаметр инопланетного Цветка Жизни достигает 1,5 км и при этом нет погрешностей, то факт первичности геометрии над материей становится очевидным. Круги на полях — поистине материальное воплощение сакральной геометрии. Причем достаточно масштабное. Интересно, что ни один фальшивый круг не содержит набора признаков, которые содержат настоящие круги на полях: в настоящих кругах дно фигуры может иметь вплоть до пяти слоев, и пшеница в каждом слое закручена в сторону, противоположную предыдущему; каждый колосок в них лежит аккуратно рядом с другим; в центре круга колосья могут хитрым образом переплестись, или же находится лишь один прямо стоящий колос или пучок колосьев. Еще одна особенность настоящих кругов на полях — это повышенное инфракрасное излучение внутри и снаружи фигуры и изменение магнитной структуры пространства. Компасы не могут определить, где север, а где юг. Камеры, мобильные телефоны и батареи не функционируют, счетчики Гейгера показывают увеличение радиации примерно в три раза по сравнению с нормальным фоном. Животные из окрестных ферм избегают мест кругов на полях еще до того, как они появятся. Настоящие круги на полях любят также располагаться поверх энергетических линий Земли, повторяя энергетический узор местности. Они могут быть «просканированы» с помощью лозы. Даже когда урожай собран и на следующий год поле снова перепахано и засеяно, лозоходец сможет определить то место, где была «инопланетная» фигура. В подавляющем числе образцов растений были обнаружены различные отклонения от нормальных форм. Стенки клеток в мембране, окружающей головки семян, были аномально увеличены. Узлы стебля искривлены и имели значительно большие размеры. Семена в колосьях или вообще отсутствовали, или у них были уродливые, недоразвитые головки. Собранные растения носят явные отпечатки воздействия кратковременных импульсов электрического поля и экстремального тепла. Такое сочетание мог дать ионно-плазменный вихрь. С помощью микроволновой радиации, возникающей вокруг ионизированной плазмы, информация наносится на круги и другие фигуры, образующие рисунки. Однако это все лишь только предположения. Несомненно одно — без матрицы сакральной геометрии здесь не обходится. Несмотря на огромное разнообразие (десятки тысяч разных фигур), у них есть четкие отличительные признаки и общие черты. Имеется тенденция преобладания похожих рисунков — треугольников, составленных из 1 большого центрального Круга и 3 маленьких Кругов, или сочетание из нескольких (от 2—3 до нескольких десятков) кругов разной величины в одной цепочке. Налицо тенденция к усложнениям рисунка, при которых все чаще проявляются самоподобность (фрактальность) и все виды симметрии (осевая, линейная, поворотная и т. д.). Если встречается цепочка глифов, то соотношения между ними практически всегда равны (каждый последующий круг больше предыдущего во столько же раз, во сколько раз он меньше последующего), либо — реже — эти соотношения подчиняются более сложному закону (коэффициент соотношений размеров увеличивается или уменьшается по какой-то математической формуле с экстремумом или без него). Иногда встречаются фрактальные рисунки: например, круги, составленные из более мелких кружков. Важная особенность всех глифов и пиктограмм: склоненные стебли никогда не упираются своими верхушками в стенки. Понятно, как это достигается в кругах и фигурах вращения — там стебли наклонены просто по часовой (реже — против). В сложных пиктограммах, казалось бы, добиться этого невозможно — если повалить стебли в виде любой линии или прямоугольной фигуры, то минимум в одной стороне четырехугольной фигуры или в одном торце отрезка стебли должны лечь в сторону стенки. Однако фигуры и линии в пиктограммах так хитро переплетаются, что этого не происходит, и «торцевые» стенки плавно переходят в отрезки, а концы отрезков — в фигуры вращения. Так или иначе, но и простые круги, и самые сложные пиктограммы не имеют ни начала, ни конца. Они как бы выполнены «одним мазком», одним непрерывающимся движением гигантского механизма. Кстати, в том же стиле построены фигуры в пустыне Наска. Как появляются круги? Обычно без лишнего шума, иногда слышен скрип. Круги, как правило, образуются за очень короткое время (от 1 секунды до нескольких минут). Нет ни одного сообщения, где этот процесс растягивался бы на больший срок. Феномен кругов не локален. После многочисленных наблюдений и протоколирования кругов в Европе было доказано, что полегание растений происходит по определенной системе, которая точно повторяется на кругах, удаленных один от другого на сотни километров, а это уже система.

Если сравнить пиктограммы, Цветок Жизни, кристаллы и снежинки, то невольно напрашивается мысль о физическом происхождении этих «цветов», без участия каких-либо других сил. Однако законы сакральной геометрии в их организации видимо придется считать первичными.

Рис. 13. Подобие форм пиктограмм на полях (а) и снежинок (б).

Стоит обратить внимание на то, что у снежинок более жесткая геометрия, чем у пиктограмм. Не потому ли, что это решетки дальнего порядка, а масштаб «исказил» и «загладил» углы этого явления? Однако нет сомнений в том, что это одно и то же явление, имеющее физическую природу с геометрическим началом. Как видим, все изображения представляют фрагменты изображения Цветка Жизни. Это происходит оттого, что древние, поняв, чем он является и насколько важен, решили сохранить его как эталон. Это потом на него стали наводить тень. Обратим внимание, что в Цветке Жизни множество незавершённых кругов, которые тоже могут быть сферами. Если просто взять и завершить все эти круги, тайна раскроется. Это был древний способ кодировки информации. Цветок Жизни традиционно изображали так потому, что тайные общества, передавая этот рисунок из рук в руки, хотели скрыть следующий образ — Плод Жизни. Стоит только завершить эти круги, как мы получим модель из тринадцати кругов, которая является одной из наиболее священных формой в Бытии. Она и называется Плодом Жизни. И именуется так потому, что она — результат, плод, из которого была создана ткань всех деталей Реальности. Все круги в этой модели — женские. Существует тринадцать способов наложения мужской энергии — иными словами, прямых линий — на эти тринадцать кругов. Если наложить на эту модель прямые линии всеми тринадцатью способами, то получится тринадцать моделей. Яйцо Жизни, тор и Плод Жизни, эти три модели в совокупности создают в Бытии все без исключения живые существа.

Если взять половину радиуса центрального круга и начертить новый круг, используя этот половинный радиус, а затем нарисовать такие же круги, расположив их по трем осям, получится Плод Жизни. Значит, пропорции Плода Жизни заложены в самом Цветке Жизни. Если проделать это еще раз, получится изображение тринадцати кругов, связанных с тринадцатью кругами, или Плод Жизни, соединенный с Плодом Жизни. Можно повторять эту операцию бессчетное число раз, в ней нет ни начала, ни конца. Подобно логарифмической спирали, которая является первичной движущейся геометрической формой Вселенной, Плод Жизни — особая сакральная фигура. Она является движущим фактором творения. Тринадцать систем информации происходят из Плода Жизни и эти тринадцать систем описывают каждый аспект нашей реальности во всех подробностях: все, о чем мы можем подумать, что можем ощутить или почувствовать, они способны проанализировать на атомарном уровне. Вы получите эти тринадцать систем, соединив мужскую и женскую геометрические энергии. Самый простой и очевидный способ привнести мужскую энергию — это провести прямые линии через центры кругов Плода Жизни. Если это осуществить, получится модель, которая во всей Вселенной известна как куб Метатрона.

Это одна из наиболее важных информационных систем во Вселенной, одна из основных моделей творения Бытия. Куб Метатрона содержится в четырех из пяти стереометрических копий Платоновых тел. Критерием Платоновых тел является равенство всех граней, поверхностей и углов, а также то, что все их вершины должны вписываться в сферу. Известны только пять геометрических тел, удовлетворяющих этим критериям. Эти фигуры были названы в честь Платона, хотя ими на двести лет раньше пользовался Пифагор, назвав их идеальными геометрическими телами. Уже в «Началах Евклида» найдено огромное количество соотношений, подтверждающих замечательный факт, что именно золотая пропорция является главной пропорцией додекаэдра и икосаэдра. Согласно комментатору «Начал Евклида» Проклу, Евклид считал венцом всех тринадцати книг своих «Начал» предложенные им способы построения пяти Платоновых тел — и именно эту важнейшую математическую информацию он поместил в последнюю, тринадцатую книгу. Тела Платона — это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета суммы плоских углов при вершине, выпуклых правильных многогранников не больше пяти. Это — правильный тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Тетраэдр — четырехгранник, все грани которого треугольники, т. е. треугольная пирамида. Правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. Куб или правильный гексаэдр — правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами. Октаэдр — восьмигранник, тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников. Додекаэдр — двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников. Икосаэдр — двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников. Куб и октаэдр дуальны, т. е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны додекаэдр и икосаэдр. Тетраэдр дуален сам себе. Правильный додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру. Так получаются из куба все остальные правильные многогранники. Сам факт существования всего пяти действительно правильных многогранников удивителен, ведь правильных многоугольников на плоскости бесконечно много! Придумать правильный тетраэдр, куб, октаэдр, по-видимому, было не трудно, тем более, что эти формы имеют природные кристаллы, например: куб-монокристалл поваренной соли (NaCl), октаэдр-монокристалл алюмокалиевых квасцов (KAl(SO4)2*12H2O). Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS). Имея же додекаэдр, нетрудно построить и икосаэдр: его вершинами будут центры двенадцати граней додекаэдра.

Это игра с линиями на бумаге. Если исчертить лист пересекающимися линиями, то, стирая их даже произвольно, можно извлечь любое, а не только Платоново тело. В Природе все происходит по этому сценарию, но гораздо проще.Вероятнее всего, в пространстве есть «заготовки» Платоновых тел, которые всегда под «рукой» для строительства того или иного объекта. Для получения Платоновых тел из Куба Метатрона нужно стереть несколько линий. Удалив некоторые линии в определенном порядке, вы вначале получите куб. Это двумерное изображение трехмерного объекта, и в нем содержится куб в кубе. Если вы сотрете другие линии в определенном порядке, то получите тетраэдр. Собственно говоря, это два сложенных вместе тетраэдра, или звезда-тетраэдрон. Два других — октаэдр в виде сложенных вместе пирамид и икосаэдр. В школах Древнего Египта и Атлантиды эти пять фигур и сфера рассматривались под другим углом. В древних школах считалось, что такие Стихии, как Огонь, Земля, Воздух, Вода и Эфир, имеют различные формы. Эти Стихии соотносились с Платоновыми телами следующим образом: тетраэдр — Огонь, куб — Земля, октаэдр — Воздух, икосаэдр — Вода и додекаэдр — Эфир, или прана. Сфера означала пустоту, из которой все происходит. Таким образом, все вещи могут быть созданы из этих форм. Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности — от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа. Что же такое многогранник? Для ответа на этот вопрос напомним, что собственно геометрию определяют иногда как науку о пространстве и пространственных фигурах — двумерных и трехмерных.

Двумерную фигуру можно определить как множество отрезков прямых, ограничивающих часть плоскости. Такая плоская фигура называется многоугольником. Многогранник можно определить как множество многоугольников, ограничивающих часть трехмерного пространства. Многоугольники, образующие многогранник, называются его гранями. Ученые издавна интересовались «идеальными» или правильными многоугольниками, т. е. многоугольниками, имеющими равные стороны и равные углы. Очевидно, что теоретически нет каких-либо ограничений на число сторон правильного многоугольника, т. е. число правильных многоугольников бесконечно.

А что такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны, как принято в математике) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой — столько же, сколько существует правильных многоугольников, т. е. при первом рассмотрении кажется, что можно создать правильный многогранник, сторонами которого может быть любой правильный многоугольник. Однако это не так. Основными числовыми характеристиками Платоновых тел является число граней F, число вершин V и число плоских углов Е на поверхности тела. Эти числовые характеристики приведены в таблице.

«Теория многогранников, в частности выпуклых многогранников, — одна из самых увлекательных глав геометрии», — таково мнение русского математика Л. А. Люстернака, много сделавшего именно в этой области математики.

Прежде всего, необходимо помнить, что геометрия додекаэдра и икосаэдра связана с золотой пропорцией. Действительно, гранями додекаэдра являются пентагоны, т. е. правильные пятиугольники, основанные на золотой пропорции. Если внимательно посмотреть на икосаэдр, то можно увидеть, что в каждой его вершине сходятся пять треугольников, внешние стороны которых образуют Пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотая пропорция играет существенную роль в конструкции этих двух Платоновых тел.

Вопрос о форме Земли постоянно занимал умы ученых античных времен. Уже Платон писал: «Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи». Эта гипотеза Платона нашла дальнейшее научное развитие в трудах физиков, математиков и геологов. Так, французский геолог де Бимон и известный математик Пуанкаре считали, что форма Земли представляет собой деформированный додекаэдр. Российский геолог С. Кислицин также разделял мнение о додекаэдрической форме Земли. Он высказал гипотезу о том, что 400—500 млн. лет назад геосфера додекаэдрической формы превратилась в геоикосаэдр.

Однако такой переход оказался неполным и незавершенным, в результате чего геододекаэдр оказался вписанным в структуру икосаэдра. В последние годы гипотеза о икосаэдро-додекаэдральной форме Земли была подвергнута проверке. Для этого ученые совместили ось додекаэдра с осью глобуса и, вращая вокруг нее этот многогранник, обратили внимание на то, что его ребра совпадают с гигантскими нарушениями земной коры (например, с Срединно-Атлантическим подводным хребтом). Взяв затем икосаэдр в качестве многогранника, они установили, что его ребра совпадают с более мелкими членениями земной коры (хребты, разломы и т. д.). Эти наблюдения подтверждают гипотезу о близости тектонического строения земной коры с формами додекаэдра и икосаэдра. Узлы гипотетического геокристалла являются как бы центрами определенных аномалий на планете: в них расположены все мировые центры экстремального атмосферного давления, районы зарождения ураганов. В одном из узлов икосаэдра (в Габоне) обнаружен «природный атомный реактор», работавший еще 1,7 млрд. лет назад. Ко многим узлам многогранников приурочены гигантские месторождения полезных ископаемых (например, Тюменское месторождение нефти), аномалии животного мира (оз. Байкал), центры развития культур человечества (Древний Египет, протоиндийская цивилизация Мохенджо-Даро, Северная Монгольская и т. п.). Все эти примеры подтверждают удивительную прозорливость интуиции Платона. Нам, как приверженцам диссимметрии, стоит задаться вопросом, а нет ли на «лике» Земли и ее проявлений? Они имеются, почти вся почва в свое время была диссимметричной и только в процессе старения стала рацемичной. Надо полагать, этот «факт» наложил отпечаток не только на кору, но и на внутренности Земли.

Долгое время считалось, что в неорганической природе почти не использовались додекаэдр и икосаэдр, имеющие так называемую пятерную или «пентагональную» ось симметрии, но пентагональная ось симметрии является постоянным «спутником» Жизни. Икосаэдр — геометрическое тело, форму которого принимают вирусы, состоящие из ДНК и белка, т. е. икосаэдральная форма и пентагональная симметрия являются фундаментальными в организации Живого вещества. Открытие квазикристаллов (основанных на икосаэдре), сделанное в 1982 г. израильским физиком Даном Шехтманом, стало выдающимся событием в современной физике, так как показало, что пентагональная симметрия и икосаэдральная форма играют большую роль в кристаллографии, что противоречило законам классической кристаллографии. В силу этого мы можем утверждать, что оси незапрещенной симметрии 2, 3, 4 и 6 порядков имеют право на существование в живых существах.

Квинтэссенцией геометрических представлений стали работы американского исследователя Д. Винтера, возглавляющего группу «Планетарные сердцебиения». Он является проповедником идеала формы, унитарного золотого сечения, которое подобно «золотой цепи» соединяет ген и Вселенную. Принимая концепцию икосаэдро-додекаэдральной формы Земли, Винтер развивает ее. Он обращает внимание на то, что угол, описываемый осью вращения Земли в ходе ее прецессии за 26 000 лет, составляет 32 градуса. Это в точности равно тому углу, под которым нужно наклонить куб, чтобы, вращая его затем вокруг оси (с пятью остановками), получить додекаэдр. По мнению Винтера, энергетический каркас Земли представляет собой додекаэдр, вставленный в икосаэдр, который, в свою очередь, вставлен во второй додекаэдр. Геометрические отношения между указанными многогранниками представляют собой золотое сечение. Додекаэдральная структура, по мнению Д. Винтера, присуща не только энергетическому каркасу Земли, но и строению Живого вещества. Так, в процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, икосаэдро-додекаэдральная структура гаструлы. Далее происходит более интересный процесс, организация биологической симметрии. Она завуалирована, но также несет в себе черты 32 классов симметрии, т. е. подчинена квантованию и простой прогрессии 2, 4, 8, 16, 32, но в основном все же пентагональной и зеркальной симметрии. Структура ДНК генетического кода Жизни также представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная — от Метагалактики до белков и ДНК — построена по одному принципу — бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения! А это основные признаки и принцип автоморфизма. Следовательно, масштаб никоим образом не влияет на Платоновы тела! Отсюда несколько необычный вывод — основой автоморфизма являются свойства Платоновых тел. Основным свойством их является заданность и неизменяемость пяти форм, независимо от их масштаба. Другой вывод — подтверждение мыслей древних греков о том, что, бесконечно деля материю, мы выйдем на простые геометрические тела. Вот так просто построены наша Вселенная и все, что находится внутри и вне ее. К сожалению, идеи геометризма были незаслуженно забыты и потерялись в тени физики. Настала пора вывести их на свет божий и придать новый импульс исследованиям в этом направлении. Однако продолжим путь по геометрическому полю. Происходят эти пять Платоновых тел из первой информационной системы Плода Жизни. Сокрытые в линиях Куба Метатрона, все эти пять форм там существуют. Додекаэдр есть завершающая фигура геометрии, и она очень важна. На микроскопическом уровне додекаэдр и икосаэдр являются относительными параметрами ДНК, планами, по которым построена вся Жизнь. Значит, в основе структуры ДНК лежит сакральная геометрия, хотя могут обнаружиться и другие скрытые взаимосвязи.

После прочитанного возникает вопрос, а имеют ли эти «игры» на бумаге какое-то отношение к физическому миру? Судя по всему, как косвенно, так и напрямую. Этот вопрос, по сути, напоминает ответ, что все построенное людьми вначале было просто мыслями, которые считаются нематериальными. Эти геометрические «кальки» копируют места соприкосновения Живого вещества с нематериальными структурами и физического мира с геометрическим. Они же указывают место контакта диссимметрии с Живым веществом. Можно даже указать место контакта. Это «линия», соединяющая бензольное и индольное кольца (Рис. 14.)

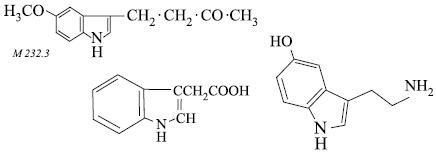
Рис. 14. Структурные формулы мелатонина, сератонина и индолилуксусной кислоты.

Подведём итог: первая информационная система выходит из Плода Жизни через Куб Метатрона. Соединением центров всех сфер вы получаете пять фигур — в действительности шесть, потому что ещё есть центральная сфера, с которой всё начиналось. Итак, мы имеем шесть первоначальных форм — тетраэдр, куб, октаэдр, икосаэдр, додекаэдр и сферу. Алхимия есть знание о том, как все эти явления удерживать в равновесии. Если вы понимаете значение этих геометрических фигур и знаете их взаимоотношения, вы можете создать то, что хотите. Вся идея заключается в понимании лежащей в основе карты. Помните, карта показывает путь, которым дух движется в Пустоте. Если вы знаете лежащую в основе карту, тогда вы обладаете знанием и пониманием, необходимым для сотворчества с Богом. Каждая вершина этих фигур связана со следующей, и все они находятся в определённых математических соотношениях, связанных с пропорцией (phi ratio).

Раньше мы рассматривали кристаллы как некую абстрактную «опору» для Живого вещества. Теперь настала пора разобраться, почему именно они, а не аморфные структуры могут быть фундаментом для Живого. В процессе кристаллизации атомы всегда выстраиваются определённым образом. Они формируются, скажем, в куб, и затем этот куб выстраивает рядом с собой другой куб и рядом с тем ещё один куб, т. е. получается куб, связанный с другим кубом, который в свою очередь связан со следующим кубом и т. д., формируя то, что именуется решёткой. Существует множество способов, какими атомы могут объединяться. Получающиеся в результате этого молекулы всегда связаны со священной геометрией и пятью Платоновыми телами. Даже проникнув в сложную молекулу и разделив её на части, можно увидеть внутри её фигуры, которые всегда соответствуют одному из пяти Платоновых тел — независимо от того, что это за структура. Неважно, металл, кристалл, что-то ещё — все всегда сводится к одной из этих первичных пяти фигур. Существуют, по крайней мере, сто тысяч кристаллов различного рода, но все они могут быть рассортированы по шести категориям: изометрические, тетрагональные, гексагональные, орторомбические, моноклинальные и триклинальные. И все эти шесть систем, используемых для классификации всех известных кристаллов, являются производными куба, одного из Платоновых тел. Важно, под каким углом вы рассматриваете куб — воспринимается ли он как квадрат, шестиугольник или прямоугольник.

Первые пять Платоновых тел представляют собой первые пять нот пентатонической шкалы. Октава содержит в себе семь нот, последние две соответствуют субоктаэдру и ромбическому додекаэдру. Пять добавочных фигур формируют хроматическую шкалу, и существует ещё тринадцатая, возвратная. Таким образом, существует 13 многогранников, которые составляют хроматическую шкалу в музыке. Из этих тринадцати образуются ещё тринадцать подобных, но — звёздные. Итак, в целом получается 26 форм — две октавы внутри друг друга. Оперируя понятиями формы, эти 26 фигур являются ключом ко всем гармониям Реальности. Посмотрим, что собой представляет число 26. Пьер Ферма доказал, что 26 — единственное число, заключенное между квадратом (25=52) и кубом (27=33). В этом случае даже нет надобности что-то дополнять.

Если бы люди знали сакральную геометрию, которая нам известна сегодня, они могли бы выйти на все 26 форм и истребить любой существующий в Бытие вирус. Не имеет значения, сколько вирусов СПИДа существует, найти разрешение ничего не стоит. Максимальное число шаблонов — 26, и соответствующие частоты истребят любой вирус или бактерию. Поскольку каждый вирус представляет собой многогранник, существует множество способов, как с ними справиться. Это несколько упрощенное понимание сути Живого вещества. Вирусы, простейшие, микробы и раковые структуры, несомненно, детерминированы сакральной геометрией. Можно сказать, что все они располагаются в разных сингониях, и переход из одной в другую знаменуется повышением их болезнетворности и злокачественности. От таких переходов естественным образом изменяется и их вибрация и структура Живого вещества. Поэтому, изменяя сингонии в Живом веществе любого уровня, можно лечить все болезни. Однако это необходимо сочетать с непосредственным воздействием на структуру белков и воды. Воздействие электромагнитной вибрацией второстепенно и может быть не эффективным ввиду того, что на разных уровнях Живое вещество нечувствительно к ним. Биофизический сдвиг в тканях живых организмов вызвать не так просто, как кажется. Это происходит по одной простой причине — живая ткань функционирует по закону автоволн и большому контуру, который описывается как S-образный закон. Поэтому воздействие ультра- и просто звука, низкоэнергетические электромагнитные волны, а также мощные скрученные магнитные поля вернут анизотропию и восстановят диссимметрию в Живой субстанции. Для этого необходимо вывести алгоритм этих вибраций для разных сингоний. Это сопряжено с большими трудностями ввиду отсутствия общей теории колебаний Живого вещества.

Данный текст является ознакомительным фрагментом.